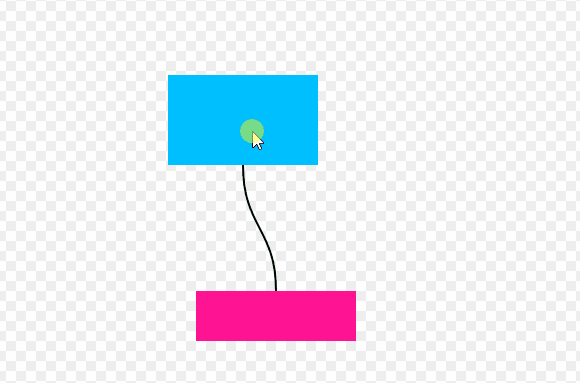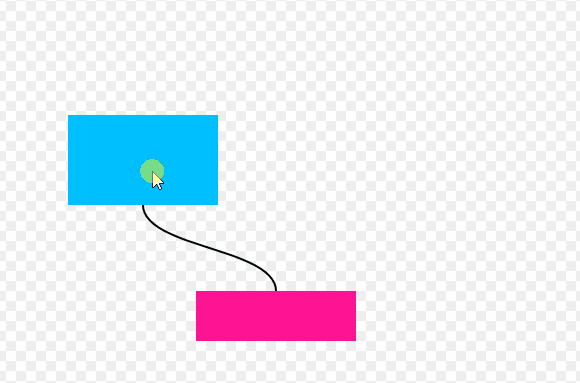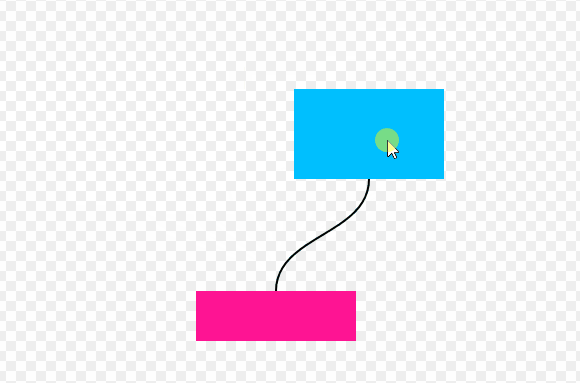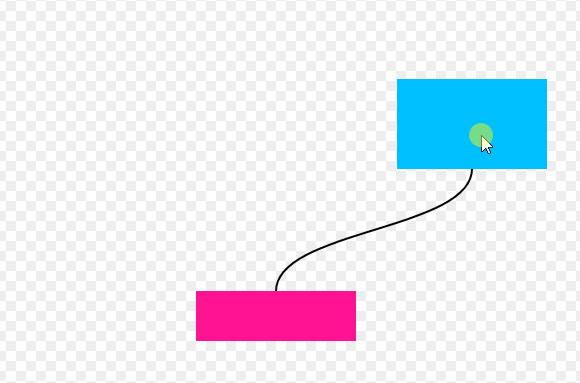
在一些在线的脑图或者流程图示意的工具中，使用曲线连接两个模块是非常常见的效果，例如figma里面的figjam。

figjam是我用过体验非常赞的一个工具，衡量自己Web前端技术的一个简单办法就是，如果让你实现这样一个产品，你能否立刻在脑中形成实现方案，并完成之。

我就想过这个问题，如果我来实现figjam，我能行吗？

突然意识到非常不确定，所谓不确定，就是还需要摸索，对能否完成，以及完成所需的时间模糊，换言之，就还是技术积累不够。

机会总是留给有准备的人的，既然自己决定深耕于交互体验领域，就必须将自己的技术缺漏补上。

如何补，很简单，聚沙成塔，也就是从一个一个的小功能的实现开始积累。

所以，我决定先研究下给任意两个点，这两个点使用贝塞尔曲线连接该如何实现。

一、任意两点之间的曲线

需求为：给定起点和终点，然后自动得到曲线

如果你使用过PS中的钢笔工具绘制过曲线，那么对里面提到的“控制点”也应该非常熟悉，基本上，脑中只要想一下起止点和控制点，曲线什么样子脑中就自动出现了，因为控制点和定位点的连线本质上是曲线的切线，所以并不难脑补。

现在起止点有了，只要知道控制点的位置，曲线自然就得到了。

理论上，控制点可以在任意位置，这就导致曲线可能千千万，所以，我们需要进行约束，增加限定条件，比方说曲线的切线是垂直的，两个控制点的垂直坐标是一致的（不一致也可以），此时的曲线效果就会如下图所示（黑色圆点是控制点）：

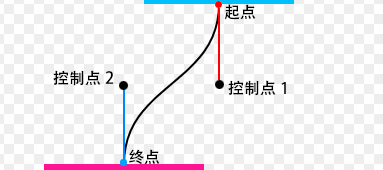
此时，控制点的位置就可以确定了，横坐标和起点或终点的横坐标一致，纵坐标在起始点之间（偏差越大，曲线曲率越大）。

算法知道了，下面就是落地成代码……

二、canvas中的曲线绘制

SVG和canvas都能绘制曲线，从易用性上讲，还是canvas更合适，其提供了原生的曲线绘制方法。

包括二次贝塞尔曲线方法 quadraticCurveTo() 和三次贝塞尔曲线方法bezierCurveTo()。

我们这里使用的是 context.bezierCurveTo()方法，语法为：

context.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y);

其中，cp1和cp2指的是两个控制点，(x, y)是结束点，起点使用 context.moveTo(x, y) 语句指定，详见我写的这个API文档。

于是我们就可以抽象出如下所示的绘制代码（假设canvas绘制的上下文对象是 context）：

var drawCurve = function (startX, startY, endX, endY) {   
    // 曲线控制点坐标
    var cp1x = startX;
    var cp1y = startY + (endY - startY) / 2;
    // 这里的除数2和曲线的曲率相关，数值绝大，曲率越小
    var cp2x = endX;
    var cp2y = endY - (endY - startY) / 2;
    
    // 开始绘制曲线
    context.beginPath();
    context.lineWidth = 4;
    context.strokeStyle = '#000';
    context.moveTo(startX, startY);
    // 绘制曲线点
    context.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, endX, endY);
    context.stroke();
};

绘制曲线，然后描边。

三、最终的实现演示

好，至于方块的绘制和拖拽，这个我早就驾轻就熟了，所以，至此，我就能确信自己可以把此交互实现了，且大概多久实现也有了预期，这样，工时评估的时候就会更加准确，日常工作也就更加从容。

所谓心中有粮，自然不慌，哦，查了下，记错了，是家中有粮，心中不慌。😅

以下就是最终实现，您可以狠狠地点击这里：JS canvas任意方块图形之间曲线连接demo

拖拽方块，可以看到曲线实时跟随，此交互效果移动端也支持，下图为GIF录屏演示：